YEJIN LEE

“Keep turnin’ the pages”

5 minute read

브루트포스 알고리즘

brute “짐승, 난폭한” + force “힘, 무력”

브루트포스 알고리즘, 완전 탐색이라고 하는 알고리즘은 모든 경우의 수를 다 탐색하여 정답을 찾는 방법이다.
투박하지만 가능한 모든 것을 탐색한다는 것으로, 그만큼 직관적이고 이해하기 쉬우며 정확한 결과값을 얻어낼 수 있다.

규칙

사용된 알고리즘이 문제를 해결할 수 있는가

효율적인가

완전 탐색은 모든 경우를 탐색하는 직관적이고 쉬운 방법인 만큼, 입력 값에 따라 시간이 매우 오래 걸릴 수 있는 단점이 있다. 따라서 이 알고리즘을 사용 시에는 문제 풀이에 효율적인지에 대한 파악이 중요하다.

완전 탐색을 사용하기 위해 다음과 같은 것들을 고려해보아야 한다.

  1. 해결하고자 하는 문제의 가능한 경우의 수를 대략적으로 계산한다.
  2. 가능한 모든 방법을 다 고려한다.
  3. 실제 답을 구할 수 있는지 적용한다.

활용 방법

  • 반복/조건문을 통해 모든 경우를 검사
  • 순열
  • 재귀호출
  • 비트마스크
  • DFS, BFS

반복 조건문을 통한 BruteForce

반복/ 조건문을 통해 가능한 모든 방법을 찾는 경우이다. 예를 들면, 0000~9999사이 모든 비밀번호를 다 입력하여 비밀번호를 푸는 방법이 이런 경우이다.




순열

순열을 배열에 순서가 있는 경우를 모두 세는 방법이다.

nPr은 n개의 수에서 r개를 순서있이 뽑아 나열하는 경우의 수임을 고등학교 수학과정에서 배운 바 있다.

순서가 있다는 것이 핵심이다.
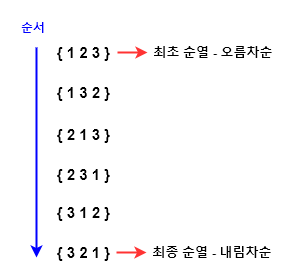
만약 수열에서 숫자 1,2,3이 있다면, 이것을 2,1,3으로 보는 것과 3,2,1로 보는 것은 차이가 있고 다름을 의미한다.

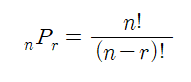
fail to bring

따라서, 만약 N개의 데이터가 있고 이를 순열을 통해 나열한다면 전체는 N! 경우가 나올 수 있다. 마찬가지로 고등학교 수학시간에 배웠을테지만 다시 한 번 언급해보면, N개의 데이터를 나열할 때, 처음엔 N개 그 다음에 올 수 있는 수 개수는 N-1개 그 다음에 올 수 있는 수 개수는 N-2개…이렇게 쭉 가서 모두 곱해주면 N!이 된다.

fail to bring

1. 재귀를 이용한 순열 - SWAP

배열들의 값을 직접 swap하는 방법으로, 배열의 첫 값부터 순서대로 하나씩 바꾸면서 모든 값을 한번씩 swap한다.

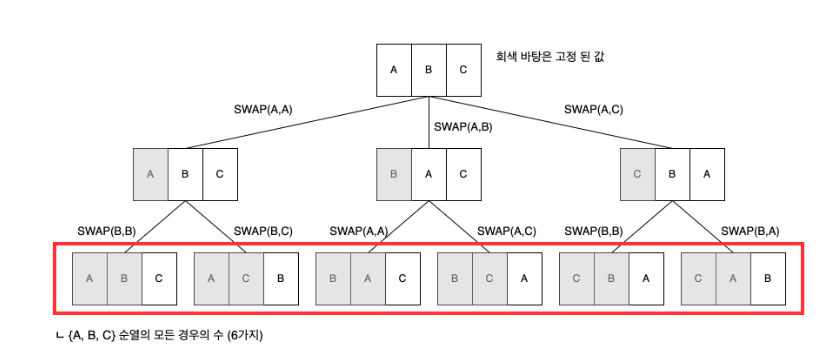
fail to bring

과정은 다음과 같다.

  1. 0번째 인덱스 원소를 0번째부터 n-1번째까지 위치를 바꾼다. abc ➡️ bac ➡️ cba를 보면 a가 0번째부터 2번째까지 모두 위치한다.
  2. 1번 과정을 진행해서 나온 경우들을 대상으로 1번처럼 똑같이 1번째 원소부터 1~n-1번째까지 위치하게 한다.
  3. 이러한 과정을 n-1번 반복한다.

이 때, 주의할 것은 순열들의 순서가 보장되지 않는다는 점인데, cab가 아니라 cba가 먼저 나오게 된다.

#include<iostream>	
#include<algorithm>
#include<vector>
#include<string>	

using namespace std;

void Permutation(vector<int> v, int Start, int End) {
	if (Start == End) {
		for (const auto data : v) cout << data;
		cout << "\n";
	}
	else {
		for (int i = Start; i <= End; i++) {
			swap(v[Start], v[i]);
			Permutation(v, Start + 1, End);
			swap(v[Start], v[i]);
		}
	}
}

코드를 설명해보면,

  1. 인자로, 배열과 순열 알고리즘의 시작 인덱스와 순열 알고리즘의 끝 인덱스를 받는다.
  2. 시작 인덱스와 끝 인덱스가 같다면, 원소가 하나이거나 모든 인덱스를 순회했다는 의미이므로 출력한다.
  3. 인덱스가 서로 다르면, 시작부터 끝가지 모든 인덱스에 대해 시작인 덱스와 자리르 바꾸고 시작 인덱스를 1만큼 이동하여 재귀 함수를 호출한 후, 다시 자리를 바꾼 인덱스와 시작 인덱스 자리를 스왑한다. 스왑한 것을 재귀호출 후 다시 스왑해주는 이유는 그 다음 탐색으로 넘어가 스왑하기 전에 원래 상태로 돌려놓기 위해서이다.

2. DFS를 이용한 순열 - visited
visited라는 배열 변수를 사용한다.

DFS(깊이 우선 탐색) 한 노드의 자식을 끝까지 순회한 후 다시 돌아와서 다른 형제들의 자식을 끝까지 타고 내려가면서 순회하는 방식

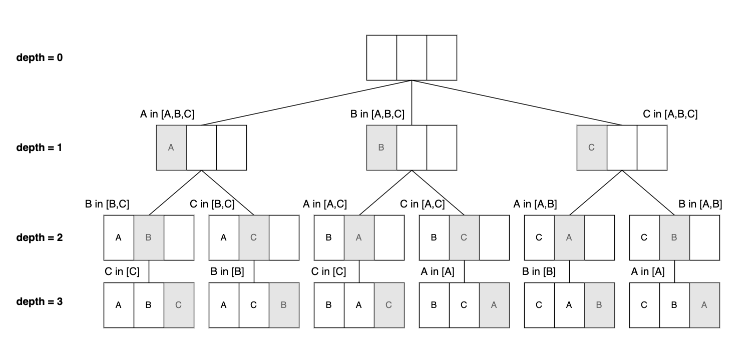
fail to bring

nPr을 생각해서, n개의 데이터 중 r개를 뽑는 과정이라고 보는 것이 낫겠다. 과정은 다음과 같다.

  1. 깊이 우선 탐색으로 돌면서 모든 인덱스에 방문해 배열에 값을 넣는다.
  2. 이미 들어간 값은 visited를 true로 변경해 중복을 방지한다.
  3. 이러한 과정을 깊이가 원하는 원소만큼(r) 뽑혔을 때와 같아질 때까지 반복한다.
void Permutaion_with_visited(vector<int> v, vector<bool> visited, vector<int> output, int depth, int n, int r) {
	if (depth == r) {
		for (const auto data : output) cout << data;
		cout << "\n";
		return;
	}
	for (int i = 0; i < n; i++) {
		if (visited[i] != true) {
			visited[i] = true;
			output[depth] = v[i];
			Permutaion_with_visited(v, visited, output, depth + 1, n, r);
			visited[i] = false;
		}
	}
}
변수 역할
v 데이터 들어가는 오리지날 수열
output 방문한 데이터를 집어넣는 곳
visited 방문했는지 안했는지 기록
n 전체 데이터 개수
depth 몇 번째까지 찼는지
r 원하는 깊이

시간복잡도 : O(n!)

재귀

말 그대로 자기 자신을 호출한다는 의미로, 위 순열을 구현한 코드에서도 볼 수 있다.

재귀를 쓰는 이유는 반복문을 아주 효과적으로 줄일 수 있기 때문이다. 숫자 N개 중에 M개를 골라 출력하는 코드를 작성할 때, 재귀를 쓰지 않는다면

  for i from 1 to 4..
      chose i
      for j from i+1 to 4..
          chose j
          print i j

이런식으로 해야할 것이다. 그런데 N과 M이 큰 숫자이면 반복문은 매우 몹시 많아질 것이다.
그러나 재귀함수를 호출 시켜 다음단계로 쉽게 넘어갈 수 있기 때문에 효율적이라고 할 수 있다.

재귀를 쓸 때 중요한 조건들이 있다.

재귀를 탈출하기 위한 종료 조건
잘못하면 무한 호출의 상태에 빠질 수 있고, 배열에서 out of Bound 에러가 날 수도 있고 잘못된 출력이 나올 수 있고 등등 문제가 많아진다.

현재 함수의 상태를 저장하는 파라미터 필요
현재 함수의 상태를 저장한다는 것은 위에서 depth변수처럼 어디까지 선택했는지, 몇 개를 선택했는지를 저장하는 것이다. 이것이 없으면 재귀 종료 조건을 만들기 힘들 것이다.

return
재귀 호출 이후 연산결과에 추가적인 연산이 필요할 수 있으므로 리턴문을 신경쓸 필요가 있다.

비트마스크

비트 연산자를 통해 부분 집합을 표현하는 방법으로, Algorithm > self study book 1에서도 다룬 바 있다. 이를 통해 부분 집합을 매우 빠르게 구할 수 있는 것을 보았다.

다시 한번 정리하자면,

And 연산(&) : 둘 다 1이면 1
OR 연산(|) : 둘 중 1개만 1이면 1
NOT 연산(~) : 1이면 0, 0이면 1
XOR 연산(^) : 둘의 관계가 다르면 1, 같으면 0
Shift 연산(«, ») : A « B라고 한다면 A를 좌측으로 B 비트만큼 미는 것이다

비트 연산의 시간복잡도는 내부적으로 상수 시간 정도로 처리되어 O(1)이라고 한다

비트 마스크는 정수로 집합을 나타내는 것이 가능하다.
예를 들어 0~9까지의 숫자로만 이루어지는 정수 집합이 있다고 할 때, 그 중 하나의 부분집합이 A = {1, 3, 4, 5, 9} 라고 가정하면, 이를 570이라는 하나의 숫자로 나타낼 수 있다.

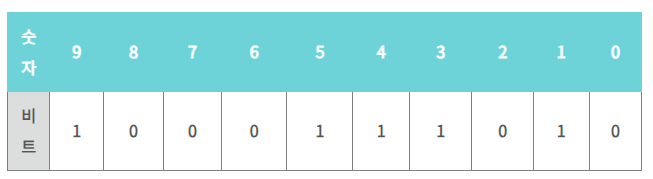
fail to bring

이렇게 표현하면 메모리도 아낄 수 있고 정수이므로 인덱스로 사용할 수도 있어서 매우 큰 장점이 된다.
비트마스크로 집합을 나타낼 때는 0~N-1까지 정수로 이루어진 집합을 나타낼 때 사용한다.

  • & 연산을 통해 해당 숫자가 현재 집합에 포함되어 있는지 검사할 수 있다.
    해당 숫자가 포함되어 있는지 검사하려면, &는 둘 다 1일때만 1을 리턴하므로 해당 숫자를 제외한 나머지를 0으로 만들고 &연산한다면 알 수 있다

  • or 연산을 통해 집합에 숫자를 추가할 수 있다.
    or연산은 둘 다 0일 때만 0을 리턴하므로, 추가하고자 하는 위치의 비트만 1로 만들고 나머지는 0이된 2진수와 or연산 한다면 추가하고자 하는 위치가 1로 변해 추가된다.

  • « 연산을 통해 부분집합 수를 구할 수 있다. 왼쪽 시프트 연산 a << b는 결과적으로 a*2^b를 계산한 값과 같다. 이는 우리가 부분집합의 개수를 셀 때 연산과 같은데, 예를 들어 4개의 데이터가 있는 집합의 부분집합 개수를 셀 때, 각 원소가 포함 될 지 안 될 지 2가지 경우를 고려해 공집합 포함 부분집합 수를 2^4개로 계산한다. 이를 이용하여 1 << 데이터 개수를 쓰면 부분 집합 개수를 빠르게 구할 수 있다.

  • ~,& 연산을 통해 특정 숫자를 제거할 수 있다. ~를 사용해 제거하고 싶은 위치의 비트만 0으로 나머지는 1로 한 뒤 &연산을 수행하면 해당 위치만 0으로 바뀌어 제거할 수 있다.

DFS, BFS

다른 페이지에 추후 업로드 후 링크 연결 예정

You may also enjoy