YEJIN LEE

“Keep turnin’ the pages”

2 minute read

1. 선택정렬

정렬할 배열이 주어졌을 때, 제일 작은 수를 찾아 맨 앞의 숫자와 바꾸며 정렬하는 방법이다.

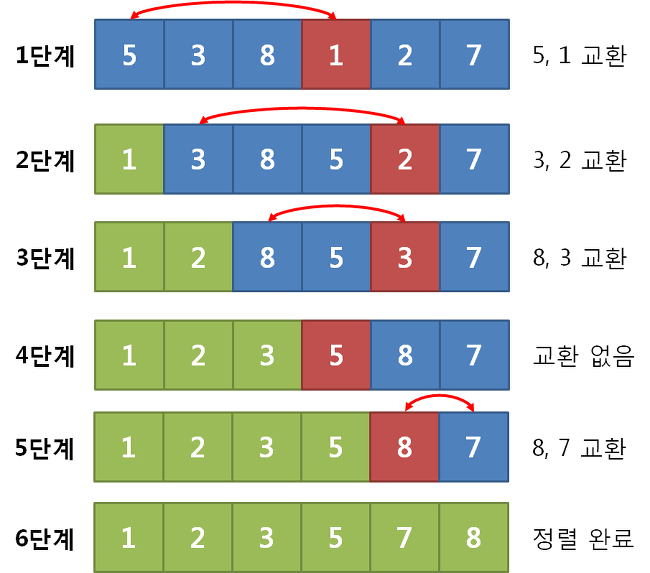
fail to bring

큰 수를 기준으로 정렬하든 작은 수를 기준으로 정렬하든 상관없다.

# selection Sort
def selection_Sort(A):
    n = len(A)
    for i in range(n-1):
        least = i
        for j in range(i+1, n):
            if A[j] < A[least]:
                least = j
            
        A[i], A[least] = A[least], A[i]

  • 참고로 파이썬에서는 스왑하는 코드가 매우 편하다

      # python swap
  a, b = b, a
  a, b, c = c, a, b

3. 문자열 매칭

4. 최접근 쌍의 거리 문제

유클리드 거리 공식을 사용하여 점 사이 거리를 구한다.

def dist(p1, p2):
    return ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5

math를 임포트 할 필요 없이 0.5재곱 해주면 된다.
이 공식을 사용해 모든 두 점의 쌍 거리를 구해 제일 작은 애를 리턴하면 된다.
기본적으로 최솟값을 구해야하므로 최솟값의 초기값을 무한대로 설정한다.

# 1. 실수값 중 제일 큰 수, 무한대
float("inf")

# 2. math를 import 하는 경우
math.inf == float("inf") # -> True
  • 튜플로 입력받는 방법
# 1. 공백으로 나눠진 정수 리스트
10 20 30 40 50 -> [10, 20, 30, 40, 50]
A = [int(n) for n in input().split()]

# 2. 공백으로 나눠진 정수 튜플
10 20 30 40 50 -> (10, 20, 30, 40, 50)
A = tuple(int(n) for n in input().split())

# 3. 공백으로 나누어진 2개의 정수 튜플
10 20 30 40 50 -> (10, 20)
A = tuple(int(n) for n in input().split()[:2])

# 4. 공백으로 나누어진 2개의 정수 튜플 3쌍

# 이때 i가 굳이 쓰이지 않는 변수일 경우, _로 써줘도 된다

편의상 튜플은 [ ]를 빼고 쓸 수 있도록 해줌. 튜플은 정의된 이후 구조를 건드릴 수 없는 상수형 리스트라고 생각하면 된다. 들어온 값에 대한 변경여부를 픽스 시킬 수 있어 조금 더 안전할 수 있다. 리스트와 튜플이 거의 비슷하기 때문에 파이썬에서는 상호대체가 가능하다. 값의 변경 여부 차이만 있다.

5. 그래프의 표현 : 딕셔너리, 집합

그래프를 나타낼 때 인접리스트(집합)와 딕셔너리를 사용한다. 리스트와 집합의 가장 큰 차이는 순서와 중복여부인데, 순서가 상관없는 경우 집합을 사용하는 것이 편하다. 범용적으로는 인접리스트로 구현하는데, 그 이유는 언어들끼리 플러그인이 편하기 때문이다.
이번에는 파이썬 셋을 사용했는데, 집합의 연산자 |(합집합), &(교집합), -(차집합)사용이 가능하기 때문이다.

파이썬 딕셔너리

  • { key1: val1, key2: val2, key3: val3, …, keyN: valN }
key in dictionary       # true, false 반환

dictionary.get(key)     # key의 value 반환/ 없으면 None 반환

dictionary.setdefault(key)
dictionary.setdefault(key, a) # key가 없으면 none을 반환하지 않고 key를 생성한 뒤 a를 value로 넣어준 뒤 a 반환
  • 문제 조건에 따라 입력받는 알고리즘
n = int(input())
for i in range(n):
    e1, e2 = input().split()[:2]

    graph[e1] = graph.setdefault(e1, set()) | {e2}
    graph[e2] = graph.setdefault(e2, set()) | {e1}

처음에는 딕셔너리에 아무것도 없기 때문에 setdefault를 사용하여 key를 정의하고 빈 집합을 주도록 한다. 그리고 방금 들어온 원소와의 합집합을 value로 준다. 결과적으로 빈 딕셔너리에 입력받은 key값을 생성하고 그 value로 집합을 만들고, value와 입력받은 원소의 합집합을 다시 key의 value로 바꿔준다. set()은 공집합이다.

You may also enjoy