YEJIN LEE

“Keep turnin’ the pages”

3 minute read

🎯깊이 우선 탐색 (DFS, Depth-First Search)

최대한 깊이 내려간 뒤, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동한다.

루트 노드에서 시작해서 다음 브랜치로 넘어가기 전에 해당 브랜치의 리프노드까지 완벽하게 탐색하는 방식이다.

하나의 방향을 결정하면 그 방향을 따라 끝까지 도달한다.

  • 트리의 경우, 왼쪽에 위치한 노드를 우선적으로 탐색한다.
  • 그래프의 경우, 가중치 또는 특정 기준을 따라 탐색 방향의 우선순위를 결정한다.

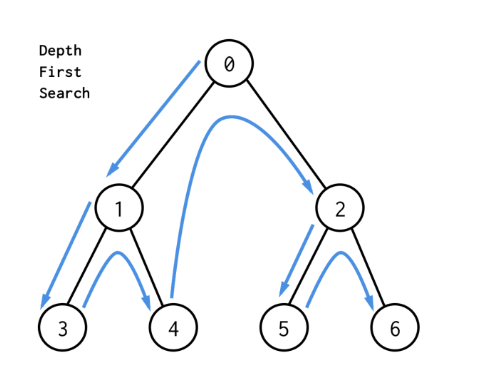
fail to bring

위의 그림으로 따지면, 0 - 1 - 3 - 4 - 2 - 5 - 6

미로찾기를 할 때 최대한 한 방향으로 쭉 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와 그 갈림길부터 다른 방향으로 다시 쭉 탐색을 진행할 수 있는 것이다.

  1. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택한다.
  2. 깊이 우선 탐색이 너비 우선 탐색보다 좀 더 간단하다.

구현은 재귀함수 혹은 스택으로 할 수 있다.

DFS - 스택

  1. 탐색 시작 노드를 스택에 삽입하고 방문 처리합니다.
  2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
  3. 2번을 계속 반복한다.

노드 방문시 visited 여부를 반드시 검사해야 한다. 무한 루프에 빠질 수 있기 때문이다.

#include<iostream>
#include<algorithm>
#include<vector>	
#include<stack>
#include<queue>

using namespace std;

int N, E, V;	// 정점 개수, 간선 개수, 시작 정점 번호

void dfs(int start, vector<int> graph[], bool visited[]) {
	stack<int> s;
	s.push(start);
	visited[start] = true;
	cout << start << " ";

	while (!s.empty()) {
		int currentNode = s.top();
		s.pop();

		for (int i = 0; i < graph[currentNode].size(); i++) {
			int nextNode = graph[currentNode][i];
			if (!visited[nextNode]) {
				cout << nextNode << " ";
				visited[nextNode] = true;
				s.push(currentNode);
				s.push(nextNode);
				break;
			}
		}
	}
}

int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> N >> E >> V;
	vector<int>* graph = new vector<int>[N + 1];	// 그래프 선언
	bool* visited = new bool[N + 1];				// 방문 유무 저장하는 배열 선언 및 초기화
	fill_n(visited, N + 1, false);

	// 그래프 입력받기
	for (int i = 0; i < E; i++) {
		int u, v; cin >> u >> v;
		graph[u].push_back(v);
		graph[v].push_back(u);
	}

	// 순차적 접근을 위해 정렬
	for (int i = 1; i <= N; i++) {
		sort(graph[i].begin(), graph[i].end());
	}
	dfs(V, graph, visited);

	return 0;
}

DFS - 재귀

void dfs_recursion(int start, vector<int> graph[], bool visited[]) {
	visited[start] = true;
	cout << start << " ";
	
	for (int i = 0; i < graph[start].size(); i++) {
		int nextNode = graph[start][i];

		if (!visited[nextNode]) dfs(nextNode, graph, visited);
	}

}

🎯너비 우선 탐색 (BFS, Breadth-First Search)

최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동한다.

루트노드에서 시작해 인접한 노드, 형제노드를 먼저 탐색하는 방식이다.
주로 두 노드 사이 최단 경로를 찾고 싶을 때 이 방법을 선택한다.

fail to bring

예를 들어, 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Sam과 Eddie사이에 존재하는 경로를 찾는 경우에,

  • 깊이 우선 탐색의 경우, 모든 친구 관계를 다 살펴야함
  • 너비 우선 탐색의 경우, Sam과 가까운 관계부터 탐색함

구현은 큐로 구현할 수 있다.

BFS - Queue

  1. 탐색 시작 노드를 큐에 삽입하고 방문 처리한다.
  2. 큐에서 노드를 꺼낸 뒤 해당 노드의 인접 노드 중에는 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
  3. 2번을 계속 반복한다.
void bfs(int start, vector<int> graph[], bool visited[]) {
	queue<int> q;

	q.push(start);
	visited[start] = true;

	while (!q.empty()) {
		int top = q.front();
		q.pop();
		cout << top << " ";

		for (int i = 0; i < graph[top].size(); i++) {
			if (!visited[graph[top][i]]) {
				q.push(graph[top][i]);
				visited[graph[top][i]] = true;
			}
		}
	}

}

DFS와 BFS

DFS BFS
현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색 현재 정점에 연결된 가까운 점들부터 탐색
스택 혹은 재귀함수로 구현 큐로 구현

시간복잡도
두 방식 모두 조건 내 모든 노드를 탐색하기 때문에 시간복잡도는 동일하다.

N이 노드, E는 간선일 때

인접리스트 : O(N+E)
인접행렬 : O(N^2)

인접 행렬은 반복문을 두 번 돌리면서 정점간 간선이 있는지 확인해야 한다. 따라서 N의 제곱만큼 시간이 소요된다.

인접리스트는 존재하는 간선의 정보만 저장되어 있으므로 반복문을 두 번 실행할 필요없이, 다음 노드가 방문되었는지 확인할 때 간선 개수 E의 두 배만큼 시간이 걸리고, 각 노드 방문할 때 정점 개수인 N만큼 걸린다. 따라서 O(N+2*E) = O(N+E)가 된다.

문제 활용

  1. 그래프의 모든 정점을 방문하는 것이 중요한 문제

  2. 경로의 특징을 저장해두어야 하는 문제

  3. 최단거리를 구하는 문제
    미로 찾기 등 최단거리를 구해야할 경우, BFS가 유리하다. 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만, 너비 우선 탐색은 현재 노드에서 가까운 곳부터 찾기 때문에 경로를 탐색 시 먼저 도달한 곳이 최단거리이기 때문이다.

참고 사이트

https://devuna.tistory.com/32
https://velog.io/@lucky-korma/DFS-BFS%EC%9D%98-%EC%84%A4%EB%AA%85-%EC%B0%A8%EC%9D%B4%EC%A0%90

You may also enjoy