[Dynamic Programming] 동적계획법 1

Dynamic Programming 동적계획법

🐦동적계획법이란 ?

복잡한 문제를 풀기 위해 간단한 여러 개의 하위 문제로 나누어 푼 다음, 그걸을 결합하여 목적에 도달하는 방법이다.

DP는

완전 검색을 하는데 좀 더 스마트하게 하는 방법이라고 할 수 있다.
Recursive + Memoization 이라고 할 수 있다.
점화식으로 표현할 수 있다.

동적계획법은 또 다시 동일한 문제를 풀 일이 없도록, 처음으로 한 번 풀었을 때, 그 결과를 배열 같은 곳에 저장해두고 동일한 문제를 만나면 배열에서 가져오는 방식으로 해결한다.

🎯토끼 수 구하기

• 첫 달에는 새로 태어난 토끼 한 쌍만이 존재한다.
• 두 달 이상이 된 토끼는 번식 가능하다.
• 번식 가능한 토끼 한 쌍은 매달 새끼 한 쌍을 낳는다.
• 토끼는 죽지 않는다.

위의 조건이 있을때, n번째 달의 토끼 수는 어떻게 될까?

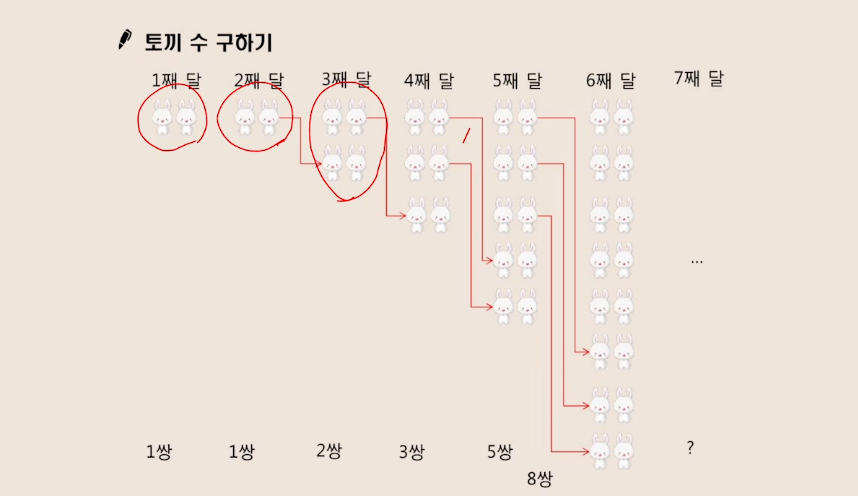
n번째 달에 a쌍의 토끼가 있고 다음 n+1번째 달에 새로 태어난 토끼를 포함해 b쌍이 있다고 가정한다면, n+2번째 달에는 a+b쌍의 토끼가 있게 된다. 왜냐하면 n+1번째에 새로 태어난 토끼는 그 다음달에 아직 번식할 수 없고 n번째 달에 있던 토끼들은 번식할 수 있기 때문에, a쌍의 토끼 수 만큼 n+2번째 달에 토끼가 더 늘어난다.

F(n)을 n번째 달의 토끼 수라고 한다면, F(n+2) = F(n) + F(n+1) 이 성립한다. ➡️ 피보나치 수열

🎯피보나치 수열

0과 1로 시작하여 이전의 두 수 합을 현재 항으로 하는 수열

피보나치 수열 i번째를 계산하는 함수 F를 정의하면 다음과 같다.
F0 = 0, F1 = 1
Fi = Fi-1 + Fi-2 for i>=2

위의 정의로부터 피보나치 수열의 i번째 항을 반환하는 함수를 재귀함수로 구현할 수 있다.

    fibo(n)  
        if n < 2: return n
        else : return fibo(n-1) + fibo(n-2)  

그러나 재귀함수로 구현하게 된다면 엄청난 중복 호출이 발생한다.

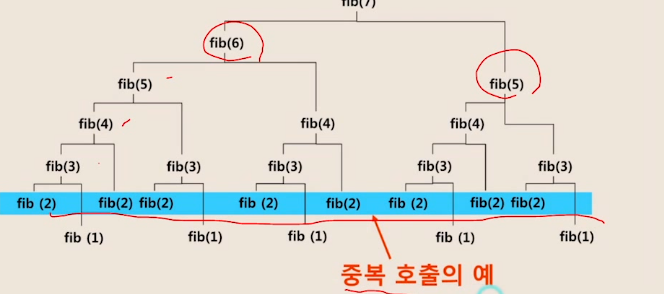
대충 두 번째가 호출되는 횟수만 봐도 약 8번이 호출된다. 겁나 많이 호출된다.

피보나치 수열을 재귀로 구현하면 얼마나 중복될까? ➡️ 수학적 귀납법 이러한 중복을 피할 수 있는 방법은 없을까?

🎯수학적 귀납법

어떤 등식이 모든n에 대해 성립함을 보이기 위해 가능한 모든n을 대입해 등식이 성립함을 모일 수는 없으므로 수학적 귀납법을 사용한다.

주어진 등식이 n = 1일 때 성립함을 증명하고, n일 때 성립한다고 가정한 후, n+1일 때 성립함을 증명한다

• 귀납 기본(Induction base): n=1에 대해 등식이 성립함을 증명
• 귀납 가정(Induction hypothesis): 임의의 n에 대해 등식이 성립함을 가정
• 귀납 단계(Induction step): 등식이 n+1에 대해서도 성립함을 증명

이를 사용해 재귀를 이용한 피보나치를 사용했을 때 얼마나 중복 호출이 일어나는지 횟수를 계산할 수 있다.

T(n) : 피보나치 n을 계산하기 위해 피보나치 함수를 호출하는 횟수

T(0) = 1;
T(1) = 1;
T(n) = T(n-1) + T(n-2) + 1(현재 함수의 항)
= 2^(n/2)

즉, 재귀적 알고리즘으로 구성한 재귀트리 마디 수를 T(n)이라고 하면, n>=2인 모든 n에 대하여 T(n) >= 2^(n/2)

🎯비둘기 집의 원리

n+1개의 물건을 n개의 상자에 넣을 때, 적어도 어느 한 상자에는 두 개 이상의 물건이 들어있다는 원리를 말한다.

귀류법으로 증명할 수 있다.

• n개의 비둘기 집과 n+1마리의 비둘기가 있다고 한다.
• 만약 가 비둘기 집에 한 마리 이하의 비둘기만 존재한다면 전체 비둘기 집에는 많아야 n마리 비둘기가 존재한다.
• 이 때, 비둘기는 n+1마리 이므로 모순.

  따라서 적어도 하나의 비둘기 집에는 두 마리 이상의 비둘기가 있다.

예시) 13명이 모였으면 같은 달에 태어난 사람이 적어도 2명 이상이다.

n번째 피보나치 수를 구하기 위해 알아야할 값은

• n이 0~n-1일 때 fibo(n)
• fibo()를 n번 호출하여 값을 알면 구할 수 있다.

이 때, 재귀로 함수를 호출할 경우 2^(n/2)이상 호출하게 된다.
따라서 비둘기 집 원리를 적용하면 중복해서 호출하고 있음을 알 수 있다.

연습문제 1

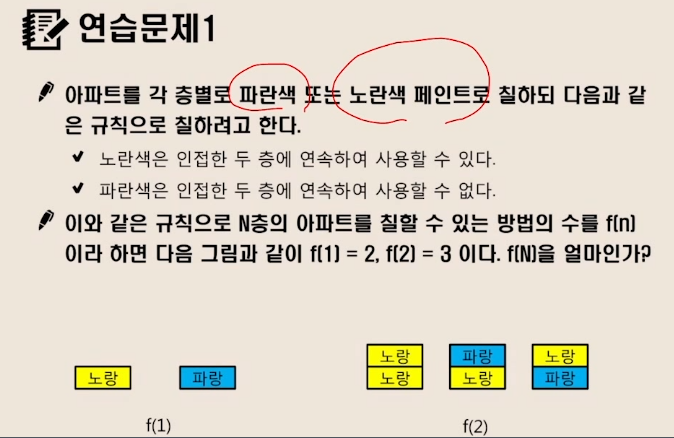
• 노란색의 경우, 이전층이 파+노인 경우 모두 가능
• 파란색의 경우, 이전층이 노랑인 경우만 가능

즉,

Yellow[n] = Yellow[n-1] + Blue[n-1]
Blue[n] = Yellow[n-1]
Yellow[1]=1, Blue[1]=1

dp[x][y] // 행은 층, 열은 마지막 층 색

dp[1][0] = dp[1][1] = 1;

for(int i = 2; i <= n; i++){
  dp[i][0] = dp[i-1][0] + dp[i-1][1]; //yellow
  dp[i][1] = dp[i-1][0];  // blue  
}

🎯메모이제이션

메모이제이션은 컴퓨터 프로그램을 실행할 때, 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술이다. 동적계획법의 핵심이 되는 기술이다.

• memoization은 글자 그대로 해석하면 메모리에 넣기(to put in memory)라는 의미로, ‘기억되어야 할 것’ 이라는 뜻의 라틴어 memorandum에서 파생되었다. 흔히 ‘기억하기’, ‘암기하기’ 라는 뜻의 memorization과 혼동하지만, 정확한 단어는 memoization이다.

피보나치 수를 구하는 알고리즘에서 값을 계산해놓고 저장하면 실행시간을 O(n)으로 줄일 수 있다.

• 추가적인 메모리 공간이 필요하다
• 재귀 함수 호출로 인한 시스템 호출 스택을 사용하게 되고 실행 속도 저하 혹은 오버플로우가 발생할 수 있다.

🐦동적계획 알고리즘

그리디 알고리즘과 같이 최적화문제를 해결하는 알고리즘이다.
최적화 문제란, 최적(최대값 혹은 최소값) 값을 구하는 문제이다. 동적 계획 알고리즘은 먼저 작은 부분의 문제에 대한 해를 구하고 이를 이용해 큰 크기의 부분 문제들을 해결하여 최종적으로 원래 주어진 문제를 해결하는 알고리즘 설계 기법이다.

동적계획법 적용 요건

동적계획법을 적용하려는 문제는 다음과 같은 요건을 만족해야한다.

1. 최적 부분 문제 구조 (optimal substructure)
   동적 계획법이 최적화에 대한 어느 문제에나 적용될 수 있는 것은 아니다. 주어진 문제가 최적화의 원칙을 만족해야 동적계획법이 효율적이다.
   최적화 원칙이란, 어떤 문제에 대해 해가 최적일 때 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것이다. 동적계획벅 방법 자체가 큰 문제의 최적 해를 작은 문제의 최적해를 이용해 도달하기 때문에 작은 문제들의 최적화 해가 아닌데 큰 문제의 최적해가 된다면 이 문제는 동적 계획법을 쓸 수 없다.

2. 중복 부분 문제 구조 (overlappint subproblems)

   • dp는 큰 문제를 이루는 작은 문제들을 먼저 해결하고 작은 문제들의 최적 해를 이용해 순환적으로 큰 문제를 해결한다. 이를 위해 점화식을 사용한다.
   • dp는 문제의 순환적 성질 때문에 이전에 계산된 작은 문제의 해를 테이블에 저장한다. 그리고 저장된 해들이 다시 필요할 때 마다 테이블을 참조하여 다시 계산하지 않고 중복을 피한다.

분할정복과 동적계획법 비교

분할정복

• 분할 정복은 연관 없는 부분 문제로 분할한다.
• 부분 문제를 독립, 재귀적으로 해결하여 해를 결합한다.

동적계획법

• 동적계획법은 부분 문제들이 연관이 있고 부분문제들은 더 작은 부분문제들을 공유한다.
• 또한 위에서 적었듯, 모든 문제를 한번만 계산하고 저장하여 재사용한다.

보통 분할 정복은 하향식, dp는 상향식으로 접근한다. dp는 부분문제들 사이에 의존적 관계가 존재하는데, 이전에 저장한 부분문제를 공유하여 각각의 문제를 풀어내기 때문이다.

DP 적용 접근 방법

1. 최적해 구조의 특성을 파악하기 문제를 부분 문제로 나눈다.

2. 최적해의 값을 재귀적으로 정의하기 부분 문제의 최적해 값에 기반해 문제의 최적해 값을 정의한다.

3. 상향식 방법으로 최적해의 값을 계산하기
   가장 작은 부분 문제부터 해를 구한 뒤 테이블에 저장하고, 점차적으로 상위 부분 문제의 최적해를 구한다.