[Eratosthenes] 아라토스테네스의 체

아라토스테네스의 체

✏️개념

• 에라토스테네스의 체는 소수(Prime Number) 를 찾는 방법이다.

• 대량의 소수들을 구해야할 때 아주 유용한 알고리즘으로 O(N^1/2)의 시간복잡도를 갖는다.

• 소수란 약수가 오로지 1인 수이다. 즉, 1을 제외한 수의 배수가 되는 수는 소수가 아니다.
  에라토스테네스의 체는 이러한 소수의 개념을 이용한 알고리즘이다.
  임의의 수 n 까지의 소수를 구하고자 할 때 2부터 n의 제곱근까지 돌며 모든 배수들을 소수에서 제외시키는 방식이다.

✏️원리

1. 배열 생성 후 초기화한다. (1은 소수가 아니니 지우고 시작)

2. 2부터 시작해서 특정 수의 배수에 해당하는 수를 모두 지운다.
   1. 2를 제외한 2의 배수를 지운다.
   2. 3을 제외한 3이 배수를 지운다.
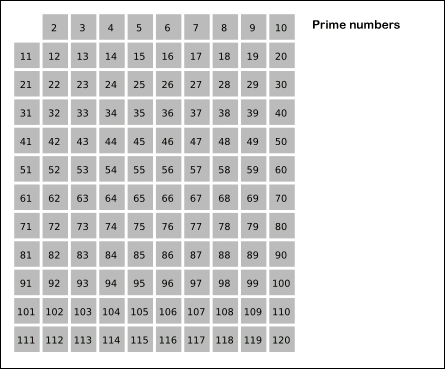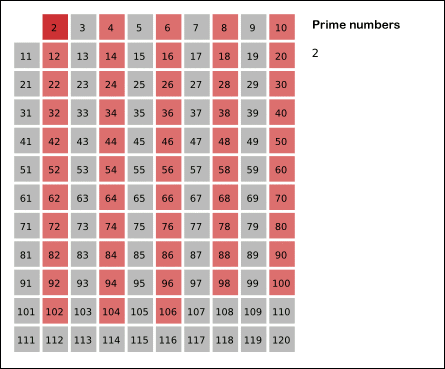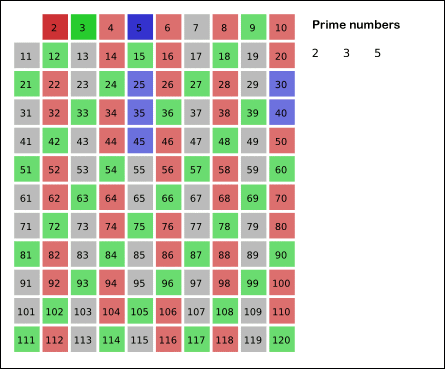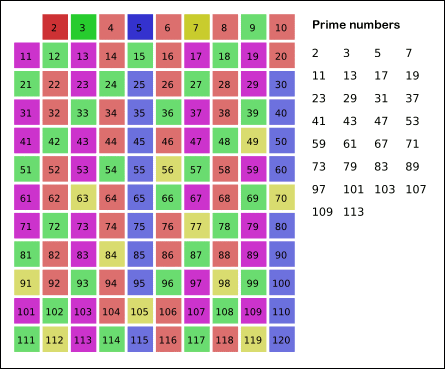
   3. 반복

3. 남아있는 수가 소수!

   

✏️코드 구현

    void PrimeNumberSieve(int N) 
        {
            int* num = new int[end + 1];
            
            //배열 초기화
            for (int i = 0; i <= N; i++) {
                num[i] = i;
            }

            //2부터 배수를 지워준다
            for (int i = 2; i <= N; i++)
            {
                //num[i] 가 0이면 이미 소수가 아니므로 continue
                if (num[i] == 0)
                    continue;

                for (int j = 2 * i; j <= N; j += i)
                    num[j] = 0;
            }

            //1은 소수가 아니므로 예외처리
            num[1] = 0;

            //출력
            for (int k = 2; k <= N; k++) {
                if (num[k] != 0) {
                    cout << num[k] << "\n";
                }
            }


        }