[Sort] 합병정렬 Merge Sort

합병정렬 Merge Sort

✏️개념

• 전체 원소를 담은 리스트를 작은 리스트 단위로 분할한 뒤에 다시 합치는 정렬

• 퀵 정렬은 피벗 값에 따라 최악의 경우 시간복잡도가 N^2이 될 수도 있지만, 병합정렬은 정확히 반씩 쪼개기 때문에 N*LogN을 보장한다.

• 퀵 정렬과 마찬가지로 분할정복 알고리즘이며, 퀵 정렬과 다르게 피벗 값이 없고 항상 반으로 나눈다.

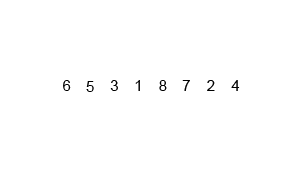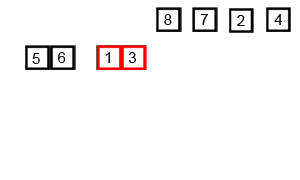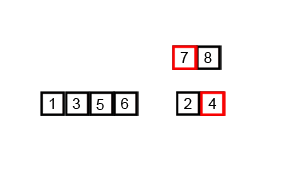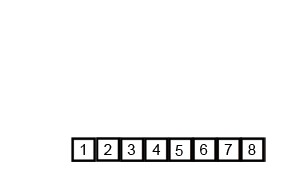
3 7 8 1 5 9 6 10 2 4

• 과정

  3 7 8 1 5 9 6 10 2 4                // 분할
  3 7 8 1 5 / 9 6 10 2 4
  3 7 8 / 1 5 / 9 6 10 / 2 4
  3 7 / 8 / 1 / 5 / 9 6 / 10 / 2 / 4
  3 / 7 / 8 / 1 / 5 / 9 / 6 / 10 / 2 / 4
  3 7 / 8 / 1 5 / 6 9 / 10 / 2 4      // 합병
  3 7 8 / 1 5 / 6 9 10 / 2 4
  1 3 5 7 8 / 2 4 6 9 10
  1 2 3 4 5 6 7 8 9 10     
  

• 높이 LogN, 너비 N 이므로 N*LogN 이 보장된다. 퀵정렬보다 빠르다고 할 수는 없지만 이 시간복잡도가 안전하게 보장된다는 것이 특징이다.

✏️구현

    #include<iostream>
    using namespace std;

    int main(void){
        int data = {1, 3, 2, 5, 4, 7, 6, 8, 10};
        int size = 9;
        int middle = (0 + size-1)/2; 

        mergeSort(data, 0, size-1);

        return 0;
    }

    void merge(int *arr, int start, int mid, int end){
        int len = arr.length();
        int* newArr = new int[len];     // 정렬되는 수들이 들어갈 배열
        int i = start;
        int j = mid + 1;
        int k = start;      // 사실상 새로운 정렬된 리스트에서 인덱스가 i와 같기 때문

        // 작은 순서대로 리스트에 삽입
        while(i <= mid && j <= end){
            if(arr[i] >= arr[j]){
                newArr[k++] = arr[j++];
            }
            else{
                newArr[k++] = arr[i++];
            }

        }

        // i혹은j 둘 중 하나가 끝난경우 남은 값을 리스트에 모두 넣어줌
        if(i > mid){
            while(j <= end){
                newArr[k++] = arr[j++];
            }
        }
        else{
            while(i <= mid){
                newArr[k++] = arr[i++];
            }
        }

        // 정렬된 배열을 전달받은 배열에 복사
        for(int t = start; t <= end; t++){
            arr[t] = newArr[t];
        }

        delete[]newArr;
    }

    void mergeSort(int* arr, int start, int end){
        if(start < end){
            int middle = (start + end)/2;
            mergeSort(arr, start, middle);
            mergeSort(arr, middle + 1, end);
            merge(arr, start, middle, end);
        }
    }

✏️시간복잡도 / BigO

• O(N*LogN)

• 기존의 데이터를 담을 추가적인 배열 공간이 필요하다는 점에서 메모리 활용이 비효율적일 수 있다.