[SWEA][Self Study Book Ⅰ] Array: 배열정의, 순열/정렬, 비트마스크/검색 및 대표문제
❗해당 내용은 SW Expert Academy에서 제공하는 학습내용을 기반으로 하고 있습니다.
1.1. Array 배열정의 및 대표문제 Gravity
🗨️들어가기
서랍장이나 물품 보관함 같은 수납장은 어디든 원하는 물건을 넣을 수 있고, 위치를 알고 있으면 원하는 물건을 꺼낼 수 있다. 반대로 특정 위치를 열어 어느것에 어느 물건이 있는지 확인 할 수 있다. 이러한 기능은 물건을 분류하거나 찾기 쉽게 만들어준다. 코딩도 마찬가지로 이런 방식으로 어떤 물건을 보관 혹은 저장하는 형태를 사용한다.
🔖대표문제 Gravity
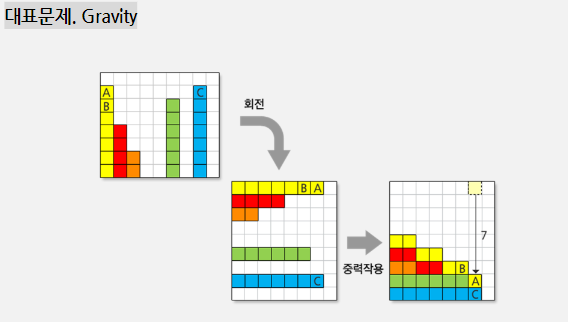
상자들이 쌓여있는 방이 있다. 방이 오른쪽으로 90도 회전하여 상자들이 중력의 영향을 받아 낙하한다고 할 때, 낙차가 가장 큰 상자를 구하여 그 낙차를 출력하여 보자.
위의 예시에서 총 26개의 상자가 최전 후, 오른쪽 그림의 상태가 된다. A상자의 낙차가 7로 가장 크므로 7을 출력하면 된다. 회전 결과, B의 낙차는 6, C 상자의 낙차는 1이다.
중력은 회전이 완료된 후 적용된다.
- 내가 생각한 방법은
먼저 보드를 2차원 배열형태(행렬 X*Y)로 만든 뒤 0으로 초기화한 상태에서 블록이 쌓여진 위치에 1을 저장한다. 그리고 행별로 마지막 열에서 시작하여 각 블록에 대한 낙차를 구한다. - 1행은 블록이 없으니 넘어가고, 2행에서는 C가 낙차가 1이 될 것이고, C부터 A까지 간격(인덱스의 차이)에 C의 낙차를 더한 값이 A의 낙차가 될 것이다. 이런 식으로 각 블록에 대한 낙차를 구한 뒤 최대값을 구하면 된다.
- 이 때 낙차를 구하기 위해서는 처음 만들어 놓은 2차원 행렬을 재탕하고, 최대값을 구하기 위해 구한 낙차값들을 따로 저장하기 위한 벡터를 만들면 될 것 같다.
📑배열
위의 문제를 풀기 위해서는 배열을 이해해야 한다.
배열을 사용하는 이유는 여러 개의 int형 변수가 필요하다고 할 때, int num0; int num1; ... int num8; 이런 식으로 변수를 선언한다면 저 변수들 사이에 어떤 수가 존재하는지 알아보려 할 때 조건문으로 일일이 하나하나 확인해야하는 귀찮은 일이 생긴다.
그러나 int arr[9]이런 식으로 배열을 선언한다면 기존보다 훨씬 간편해진다. 또한 배열은 연속적으로 메모리가 할당되기 때문에 인덱스를 사용하여 차례차례 접근하기 쉬워진다.
Arr[0] =10; for(int i=0; i<arr.length();i++ 이렇게 간결하게 사용할 수 있다.
추가적으로 2차원 배열을 선언할 수 있는데, 그렇다고 배열이 실제로 2차원 공간에 메모리가 할당 되는 것은 아니다. 만약 Arr[4][5] 선언했을 때, 4*5만큼 크기가 메모리에 연속적으로 할당되고, 코딩을 할 때 개발자들이 좀 더 편리하게 2차원적 개념으로 변수에 접근할 수 있게 된다.
마찬가지로 2차원 배열만이 아니라 다차원 배열을 선언할 수 있으며, 이를 활용하여 다양한 문제 풀이 전략을 세울 수 있다.
⚙️대표문제 Gravity 해결하기

입력
첫 번째 줄에 test case의 수 T(1≤T≤100) 가 주어진다. 각 케이스의 첫째 줄에 방의 가로 길이 N(2≤N≤100)과 방의 세로 길이 M(2≤M≤100) 이 주어진다. 다음 줄에는 N개의 상자들이 쌓여 있는 높이 H(0≤H≤M)가 주어진다.
1 // 테스트케이스T의개수
9 8 // 방의가로길이N, 방의세로길이M
7 4 2 0 0 6 0 7 0 // 상자들이쌓여있는높이
출력
낙차가 가장 큰 값을 출력 한다.
7
해설
방은 2차원 배열을 사용하여 저장한다. 또한 오른쪽으로 90도 회전 한 값을 따로 저장하는 방법보다는 입력으로 받은 값을 회전했다고 취급한다. 회전은 2차원 배열에서 행과 열이 바뀌는 것과 같다.
해설에서 설명한 가장 쉽게 생각할 수 있는 방법은 내가 위에서 생각한 방법처럼 2차원 배열을 선언한 뒤 상자를 1과 0으로 채우는 것이다.
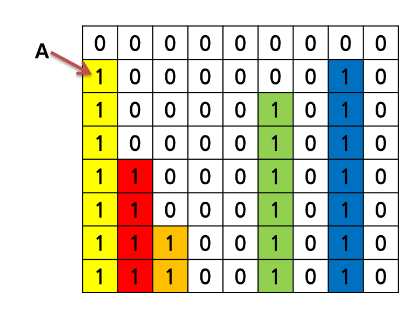
방이 오른쪽으로 회전하면 상자들이 오른쪽 정렬되는 것과 같다. 따라서 상자 오른쪽에 있는 빈칸 개수가 이동하는 거리와 같다. 나는 맨 오른쪽 상자부터 낙차를 구해 왼편에 있는 블록과 인덱스 차이를 더해가며 블록의 낙차를 구해가는 생각을 했는데 그게 생각해보니 0의 개수와 같은 것이었다. 따라서 오른쪽 빈칸 수를 각 블록에 대해 구하고 최댓값을 구하면 된다.
이 방법은 시간 복잡도가 O(n^3)이다. 빠른 건 아니고 방의 크기가 커지면 꽤 오래 시간이 걸릴 것이다.
조금 더 생각해보면 사실 낙차가 가장 큰 상자는 위쪽에서 나올 확률이 크다는 것이다. 가장 최대값의 낙차를 가지려면 가장 위의 상자만이 최대 낙차를 가질 수 있다는 특징을 알아낸다면 더 효율적으로 빠르게 풀 수 있다.
이런 식으로 문제를 풀 때 내가 직접 문제를 푸는 머릿속 사고 과정이 알고리즘이 될 수 있지만, 더 나아가 답이 될 수 있는 특성을 생각해보는 것이 꼭 필요하다.
Code
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define EMPTY 0
#define BOX 1
int main(void) {
int T = 0; // testcase
int roomWidth, roomHeight = 0; // width, height of room
cin >> T;
for (int t = 0; t < T; t++) {
vector<int> tmp;
vector<int> boxHeight; // height of boxes
vector<vector<int>>room;
int countOfEmpty = 0;
int max = 0;
cin >> roomWidth >> roomHeight;
// 방 초기화
for (int i = 0; i < roomHeight; i++) tmp.push_back(EMPTY);
for (int i = 0; i < roomWidth; i++) room.push_back(tmp);
// 상자 채우기
for (int i = 0; i < roomWidth; i++) {
int H; cin >> H; boxHeight.push_back(H);
for (int j = 0; j < H; j++) {
room[i][j] = BOX;
}
}
// 각 열마다 맨 위 상자의 낙차를 구한다
for (int i = 0; i < roomWidth; i++) {
if (boxHeight[i] > 0) {
countOfEmpty = 0;
for (int j = i + 1; j < roomWidth; j++) {
if (room[j][boxHeight[i] - 1] == EMPTY) countOfEmpty++;
}
if (max < countOfEmpty) max = countOfEmpty;
}
}
cout << max << endl;
}
return 0;
}
인덱스를 다루는 것은 언제나 헷갈리기 때문에 차분히 그림으로 놓고 생각해보는 것이 도움이 된다.
위의 코드에서는 문제를 풀기 위해 2차원 배열 사이즈를 만들고 초기화 할 때, width가 세로가 되고 height가 가로가 되도록 했다. 행과 열 위치를 바꾼셈. 오른쪽으로 회전한 모양으로 초기화하고 상자를 채워준 셈이 된다.
1.2. 순열과 정렬 및 대표문제 Baby Gin Game
🔖대표문제 Baby-Gin Game
0~9 사이의 숫자 카드에서 임의의 카드 6장을 뽑았을 때, 3장의 카드가 연속적인 번호를 갖는 경우를 run, 3장의 카드가 동일한 번호를 갖는 경우를 triplet이라 한다.
그리고 6장의 카드가 run과 triple로만 구성된 경우를 BaybyGin이라고 하는데, 6자리 숫자를 입력받아 Baby-gin 여부를 판단하는 프로그램을 작성해보자.
예시
- 667767은 두 개의 triplet 이므로 Baby-Gin (666,777)
- 054060은 한 개의 run과 한 개의 triplet이므로 Baby-Gin(456, 000)
- 101123은 한 개의 triplet이 존재하나, 023이 run이 아니므로 Baby-Gin이 아니다.
⚡내가 생각한 방법
6자리 숫자를 입력 받았을 때 각 자리수를 저장하는 것부터 생각해보자.
- 숫자를 입력받아 벡터에 저장하고 오름차순으로 정렬
- 정렬을 생각한 이유는 연속적이거나 동일한 번호를 갖는지 생각할 때, 정렬해 놓은 뒤 보면 쉽게 알아볼 수 있기 때문이다.
- 세 자리 / 세 자리 나누어 run 혹은 triplet인지 검사
- 만약 정렬한 수가 122223이면 앞 뒤 세 자리로 나누어 검사할 땐 아무것도 해당하지 않지만 실제로는 Baby-Gin인 문제가 발생한다. 정렬하고 unique를 사용하여 중복되는 수는 뒤로 빼는 방법을 사용해야 할 것 같다.
가장 떠올리기 쉬운 방법은 모든 경우의 수를 나열하고 확인 해보는 브루트포스(완전탐색)이다.
일반적으로 경우의 수가 상대적으로 적을 때 유용하고 오답의 가능성이 매우 낮기 때문에 어떤 문제를 해결하기 위해 접근한다면 이 알고리즘이 적합하다.
마찬가지로 Baby-Gin도 경우의 수가 많이 나오지 않기 때문에 답을 도출하기 적합하다.
나열 가능한 모든 방법으로 나열하고 앞 세 자리와 뒤 세 자리를 잘라 run과 triple여부를 확인하고 판단한다.
완전탐색은 이 문제처럼 입력 값이 작은 경우에만 빠른 시간내 답을 출력한다는 단점이 있다.
📑순열
위 문제에서 완전탐색을 통해 접근할 때 시간복잡도 계산을 위해서는 순열을 알아야한다.
nPr = n(n-1)(n-2)(n-3)…(n-r+1) = n! / (n-r)!
O(n!)
n!의 시간복잡도는 매우 오래 걸리는 수준이다.
따라서 위의 방법으로 시도할 경우 입력 값이 커지면 출력까지 너무 오랜 시간이 걸린다.
📑정렬의 종류
- 버블 정렬
- 카운팅 정렬
- 선택 정렬
- 퀵 정렬
- 삽입 정렬
- 병합 정렬
여기선 버블 정렬과 카운팅 정렬만 간단히 정리한다.
버블 정렬

버블 정렬이란 인접한 두 개의 원소를 비교하며 자리를 계속 교환하는 방식을 말한다.
시간복잡도는 O(n^2)
느리지만 코드가 단순해 자주 이용된다.
- 첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하며 맨 마지막 자리까지 이동한다
- 한 단계 끝나면 가장 큰 원소가 마지막 자리로 정렬된다
- 교환하며 자리를 이동하는 모습이 거품이 물 위로 올라오는 것과 같아서 버블 정렬이다
구현
for(int i = 0; i < arr.length() - 1; i++){
for(int j = 0; j < arr.length() - 1 - i; j++){
if(arr[j] > arr[j+1]){
int tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = arr[j];
}
}
}
- 배열 원소 크기만큼 반복한다
- 반복하며 가장 큰 원소는 정렬되므로 가장 큰 원소를 제외한 만큼 반복한다
- 오른쪽 원소가 더 작으면 왼쪽과 swap한다
카운팅 정렬
카운팅 정렬이란 항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 세는 작업을 하여 선형 시간에 정렬하는 효율적인 알고리즘이다.
n이 리스트 길이, k가 정수의 최댓값이라 하면 시간 복잡도는 O(n+k)가 된다. 버블 정렬과 달리 교환하지 않지만,
n이 비교적 적을 때만 가능하다.
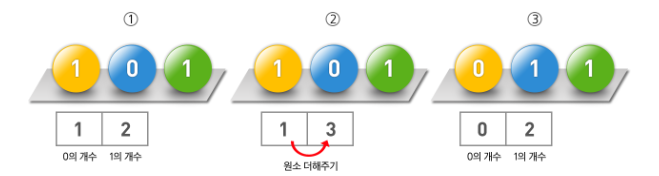
과정을 크게 세 가지이다.
- 배열 내 각 항목이 몇 개씩 있는지 파악
- 이전의 원소 개수만큼 이후 배열 값에 더해줌
- 정렬할 원소와 각 원소의 개수를 저장한 배열을 통해 정렬
특징은 다음과 같다.
- 정수형에 대해서만 가능하다.
- 카운트를 위해 충분한 공간을 할당하려면 집합 내 가장 큰 정수를 알아야 한다.
- 속도가 빠르고 안정적이다.
구현
// 각 원소 개수 세기
for(int i=0; i < arr.length(); i++){
if(maxVal < arr[i]) maxVal = arr[i];
counts[arr[i]]++;
}
// 각 원소 위치를 위해 카운트 조정
for(int i=1; i <=maxVal; i++){
counts[i] = counts[i] + counts[i-1];
}
// 카운트를 사용해 각 항목 위치 결정
for(int i=arr.length()-1; i >= 0; i--){
temp[--counts[arr[i]]] = arr[i];
}
- arr배열에는 정렬할 날 것의 데이터가 들어있다.
- arr을 순회하면서 각 원소 개수를 카운팅하여 counts배열에 저장한다.
-
정렬된 집합에서 각 항목의 앞에 위치할 개수를 반영하기 위해 counts를 조정한다.
index 0 1 2 3 4 arr = { 0, 4, 1, 3, 1 } counts = { 1, 2, 1, 1, 0 } 조정하면 counts = { 1, 3, 4, 5, 5 } -
temp배열에 원소들을 정렬하는데, arr의 역순으로 내려온다
index 0 1 2 3 4 arr = { 0, 4, 1, 3, 1 } counts = { 1, 3, 4, 5, 5 } temp = { 1 } counts = { 1, 2, 4, 5, 5 } arr=1 temp = { 1 3 } counts = { 1, 2, 4, 4, 5 } arr=3 temp = { 1 1 3 } counts = { 1, 1, 4, 4, 5 } arr=1 temp = { 1 1 3 4 } counts = { 1, 1, 4, 4, 4 } arr=4 temp = { 0 1 1 3 4 } counts = { 0, 1, 4, 4, 4 } arr=0
버블: O(n^2) 코드가 간단
카운팅: O(n+k) n이 비교적 작을 때만 가능
이를 통해 Baby-Gin문제를 풀어보려면, 대부분 옳은 결과를 낼 수도 있으나, 일부 input에는 오답을 출력한다. 위에서 내가 고려했던 input과 비슷하다.
123123을 정렬하면 112233이 되는데 결과와 답이 다르다.
증명 없이 접근하여 오답을 발생시키는 것이다. 이러한 접근 방식을 탐욕 알고리즘이라고도 한다.
탐욕알고리즘
이미 많이 다루었기 때문에 간단히 정리하고 넘어가자면,
최적 해를 구하는데 사용되는 근사 알고리즘으로, 선택할 수 있는 여러 경우 중 하나를 선택할 때 가장 최적이라고 생각되는 것을 선택해 나가는 방식으로 최종적인 해답에 도달하는 방법이다.
각 선택의 시점에서는 지역적으로 최적이지만 최종적으로는 최적이라는 보장이 없다.
일반적으로 머리 속에 떠오르는 생각을 검증 없이 바로 구현할 경우 탐욕 알고리즘적 접근이 되는 경우가 있다
⚙️대표문제 Baby-Gin
탐욕 알고리즘으로 풀어보자.
0~9 사이의 숫자 카드에서 임의의 카드 6장을 뽑았을 때, 3장의 카드가 연속적인 번호를 갖는 경우를 run, 3장의 카드가 동일한 번호를 갖는 경우를 triplet이라 한다.
그리고 6장의 카드가 run과 triple로만 구성된 경우를 BaybyGin이라고 하는데, 6자리 숫자를 입력받아 Baby-gin 여부를 판단하는 프로그램을 작성해보자.
입력
첫 번째 줄에 test case의 수 T(1≤T≤100) 가 주어진다. 각 케이스는 6자리 숫자가 들어온다
3
667767
054060
101123
출력
Baby-Gin 아니면 Lose를 출력한다.
BabyGin
BabyGin
Lose
해설
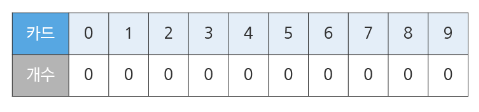
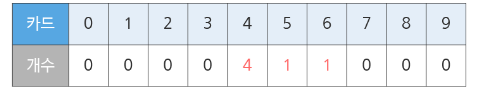
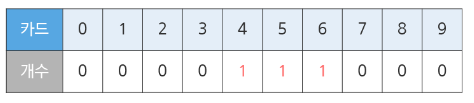
각 카드가 있는 개수를 저장하는 배열을 만들고, 입력된 숫자 개수를 저장한다.
0부터 확인하며 3이상의 수가 있는지 확인해보는데, 3개 이상 있다는 것은 triple이 존재한다는 것이다.
진행하면서 개수가 1 이상 등장할 경우 연속 세 개가 1이상인지 판단하고 run을 검사한다.
Code
/*
0~9 사이의 숫자 카드에서 임의의 카드 6장을 뽑았을 때, 3장의 카드가 연속적인 번호를 갖는 경우를 run,
3장의 카드가 동일한 번호를 갖는 경우를 triplet이라 한다.
그리고 6장의 카드가 run과 triple로만 구성된 경우를 BaybyGin이라고 하는데,
6자리 숫자를 입력받아 Baby-gin 여부를 판단하는 프로그램을 작성해보자.
*/
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main(void) {
int Testcase = 0;
cin >> Testcase;
bool tri, run = false;
for (int t = 0; t < Testcase; t++) {
int arr[10] = { 0 }; // 배열 초기화
int num = 0; cin >> num;
// 각 카드 입력받고 개수 저장
for (int i = 0; i < 6; i++) {
arr[num % 10]++;
num /= 10;
}
//triple 조사
for (int i = 0; i < 10; i++) {
if (arr[i] >= 3) {
arr[i] -= 3;
tri = true;
i--;
}
if (arr[i] >= 1 && arr[i + 1] >= 1 && arr[i + 2] >= 1) {
arr[i]--; arr[i + 1]--; arr[i + 2]--;
run = true;
i--;
}
}
if (tri && run) cout << "Baby Gin";
else cout << "Lose";
}
return 0;
}
1.3. 비트연산자와 검색 및 대표문제 부분집합의 합
🔖대표문제 부분집합의 합
유한 개의 정수로 이루어진 집합이 있을 때, 이 집합의 부분 집합 중에서 그 집합의 원소를 모두 더한 값이 0이 되는 경우가 있는지를 알아내보자.
예를 들어,
{ -7, -3, -2, 5, 8 }
이라는 집합이 있을 때, {-3, -2, 5}는 이 집합의 부분 집합이면서 총 합이 0이므로 이 경우의 답은 참이다.
생각해봅시다
부분집합을 만드는 경우를 순열로 생각해본다면, 각 원소가 들어갈지 말지 정하는 것이므로 원소 개수가 n개이면 2^n개가 나오고, 즉 모든 부분집합을 저장하고 0이 되는지 아닌지 확인하는 완전탐색으로 접근한다면 시간이 꽤 오래 걸릴 수 있다.
완전기법으로 풀기 위해 다중 for문이나 재귀호출을 사용한다면, 원소의 개수에 따라 for문의 개수가 달라지므로 비효율적이고 원소 개수에 따라 시간이 너무 오래걸려 비효율적이다.
각 원소가 부분집합에 들어갈지 아닐지를 0과 1로 표현한다면, 비트 연산자를 이용하여 주어진 집합의 부분집합들을 2진수로 표현할 수 있게 된다. 2진수로 표현된 뒤 비트연산을 통해 모든 부분집합을 구하는 것이 가능하다.
📑비트연산자
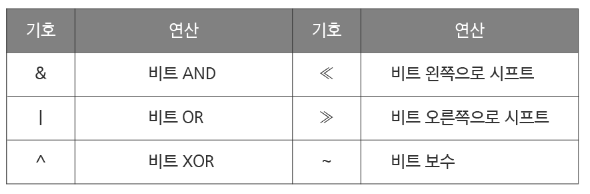
- AND: 모두 1이 있을 때만 1
0101 & 0011 == 0001 - OR: 하나라도 1이 있으면 1
0101 | 0011 == 0111 -
XOR: 둘 다 0 또는 1이면 0 다르면 1
0101 ^ 0011 == 0110 - 비트 왼쪽 시프트
<<: 숫자의 모든 비트를 왼쪽으로 옮기고 빈 비트 자리를 0으로 채운다a*(2^b)
0101 « 1 == 1010
- 비트 오른쪽 시프트
>>: 모든 비트를 오른쪽으로 옮긴다a/(2^b)
0101 » 1 == 0010
- 비트 보수
~: 모든 비트를 뒤집어 반대로 나타낸다
~0101 == 1010
⚙️대표문제 부분집합의 합
유한 개의 정수로 이루어진 집합이 있을 때, 이 집합의 부분 집합 중에서 그 집합의 원소를 모두 더한 값이 0이 되는 경우가 있는지를 알아내보자.
예를 들어,
{ -7, -3, -2, 5, 8 }
이라는 집합이 있을 때, {-3, -2, 5}는 이 집합의 부분 집합이면서 총 합이 0이므로 이 경우의 답은 참이다.
입력
첫 줄에는 테스트케이스 개수 N이 주어진다. 이후 N줄에 걸쳐 테스트케이스가 주어진다. 각 테스트 케이스의 처음에는 집합에 포함된 원소의 개수가 주어지고 이수원소가 입력으로 주어진다.
1
5 -7 -3 -2 5 8
출력
각 테스트케이스에 대하여 집합의 원소를 모두 더한 값이 0이 되는 경우가 있으면 True를 출력하고, 없다면 False를 출력하라.
True
해설
비트 연산자를 사용하여 위 문제를 보다 간결하게 만들 수 있다.
- 1 « n: 2^n 즉, 원소가 n개일 경우 모든 부분집합의 수를 계산할 수 있다.
- i&(1 « j): i의 j번째 비트가 1인지 아닌지를 리턴한다.
code
#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
using namespace std;
int main(void) {
int i, j;
int arr[] = { -7, -3, -2, 5, 8 };
int n = sizeof(arr) / sizeof(arr[0]); // 원소 개수
int sum, ret;
for (i = 1; i < (1 << (n)); i++) { // 1 << n == 2^n : 부분집합의 개수
sum = 0;
for (j = 0; j < n; j++) {
if (i & (1 << j)) sum += arr[j];
}
if (sum == 0) {
ret = 1;
break;
}
}
ret ? cout << "True" : cout << "False";
return 0;
}
- 배열의 길이를 n에 저장하고
- 부분 집합 개수만큼 반복시킨다
i를 2진수로 표현했을 때, 각 비트가 부분집합의 포함여부를 나타내는 것이다i는 1부터2^n - 1까지 증가하는데, 이는 모든 원소를 포함하지 않는 빈 부분 집합을 제외한 모든 부분 집합을 나타낸다- n이 여기선 5이므로
i는 1부터 31까지 증가하며 이진수로 표현하면 00001, 00010, … , 11111이 된다.
- 원소의 수만큼 비트를 비교한다
j는 0부터 n-1까지 반복하면서i의 비트 표현에서 1인 위치에 해당하는 배열 원소를 더한다
- 합이 0이 되는 부분집합이 있으면 반복문을 빠져나와 결과를 반환한다
📑검색
검색이란? 저장되어 있는 자료 중에서 원하는 항목을 찾는 작업을 말한다.
- 순차 검색
- 이진 검색
- 해싱
순차 검색
Sequential Search 순차 탐색이란 일렬로 되어 있는 자료를 순서대로 검색하는 방법이다.
- 가장 간단하고 직관적인 검색 방법
- 배열이나 연결 리스트 등 순차구조로 구현된 자료구조에서 원하는 항목을 찾을 때 유용
-
알고리즘이 단순하여 구현은 쉽지만, 검색 대상의 수가 많으면 시간이 급격히 증가해 비효율적
정렬되어 있지 않은 경우
- 첫 번째 원소부터 순서대로 검색 대상과 키 값이 같은 원소가 있는지 비교하며 찾는다
- 키 값이 동일한 원소를 찾으면 그 원소의 인덱스를 반환한다
- 자료구조의 마지막에 이를 때까지 검색 대상을 찾지 못하면 검색에 실패한다
찾고자 하는 원소의 순서에 따라 비교회수가 달라지는데, 정렬되지 않은 자료에서 순차탐색의 평균 비교회수는
1/n(1 + 2 + 3 + … + n) == (n+1)/2
O(n)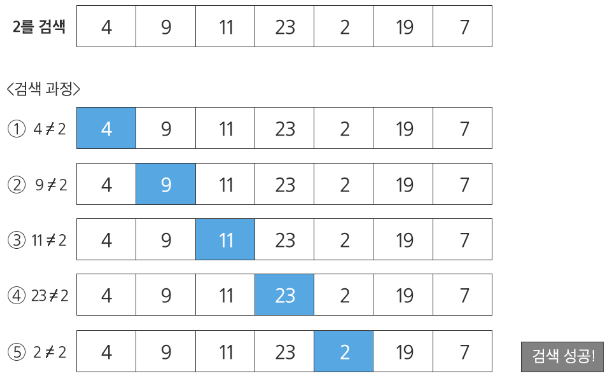
int sequentialSearch(int arr, int num, int key){ for(int i = 0; i < num; i++){ if(arr[i] == key) return i; } return -1; }
이진 검색
Binary Search 이진 탐색이란 자료의 가운데에 있는 항목의 키 값과 비교한 다음 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법이다. 목표 키를 찾을 때까지 이진 검색을 순환적으로 반복하면서 검색 범위를 반으로 줄어가며 빠르게 검색을 할 수 있다.
이러한 이진 탐색을 성공적으로 수행하기 위해서는 자료가 정렬된 상태이어야 한다.
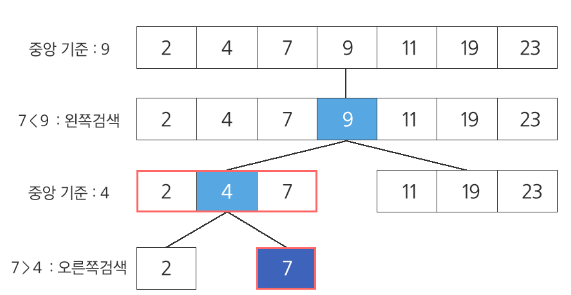
탐색 순서
- 자료 중앙 원소를 고르고 찾고자 하는 값인지 비교
- 목표 값이 중앙 원소의 값보다 작으면 자료의 왼쪽 반, 크면 오른쪽 반에 대해 검색
- 위의 과정 반복
int binarySearch(int arr, int num, int key){
int up, mid;
int down = 0;
up = num - 1;
for(;;){
mid = (up + down)/2;
if(arr[mid] == key) return mid;
if(arr[mid] > key) up = mid -1;
else down = mid + 1;
if(up < dowm) return -1;
}
}