[SWEA][Self Study Book Ⅰ] Array: 배열순회/선택정렬 및 대표문제
❗해당 내용은 SW Expert Academy에서 제공하는 학습내용을 기반으로 하고 있습니다.
1.4. 배열의 순회와 선택정렬 및 대표문제 Ladder
🔖대표문제 Ladder
사다리게임에서 꽝에 도착하게 되는 출발점을찾아라. 꽝은 2로 표시한다.
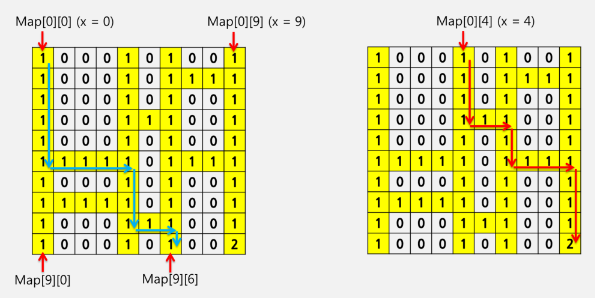
X=0 인 출발점에서 출발하는 사례에 대해서 화살표로 표시한 바와 같이, 아래 방향으로 진행하면서 좌우방향으로 이동가능한 통로가 나타나면 방향전환을 하게 된다.
방향 전환 이후엔 다시 아래 방향으로만 이동하게 되며, 바닥에 도착하면 멈추게 된다.문제의 X표시에 도착하려면 X=4 인 출발점에서 출발해야 하므로 답은 4가 된다.
생각해봅시다
꽝인 부분부터 역으로 올라가야 할 것 같다. 정상적인 사다리 타기 방향은 아래, 좌, 우 세 가지인 셈이다. 위로 올라가는 건 방향이 위, 좌, 우로 마찬가지로 세 가지. 위로 한 칸 씩 올라가면서 오른쪽 혹은 왼쪽으로 갈 수 있는지 검사하고 갈 수 있으면 그쪽으로 이동. 위로 이동할 수 있는지 검사하면서 이동한다.
보드는 2차원 배열로 만들 것이고, 그림과 같이 꽝은 2로 해놓는다.
즉, 꽝을 찾는 프로그램을 만들으려면 좌우로 이동할 수 있는지 검사하는 기능이 핵심 아닐까?
힌트
위 문제 풀이 방법은 크게 두 가지가 있다.
- 전체 시작 점을 순차적으로 끝 점에 도달하는 지 검사
- 끝점에서 거꾸로 시작지점으로 도달하는 지 검사 ⬅️이게 내가 생각한 방법
둘 다 어느 사다리를 고르면 목표지점인 꽝에 도달하는지 알 수 있지만, 1번은 너무 많은 시간이 걸리므로 최적은 2번이다.
사다리는 2차원 배열로 표현할 수 있으며 순회를 할 때, 주어진 조건인 이동하는 중 왼쪽 혹은 오른쪽 사다리를 만나면 이동하는 것을 포함시킬 것이다.
📑배열의 순회
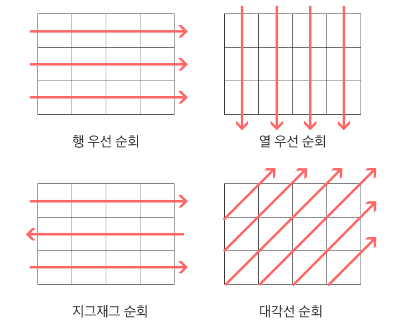
배열의 순회는 n이 자연수 일 때, 모든 n차원의 배열에서 일어날 수 있다. 순회의 목적은 어떤 값을 찾거나, 정렬 등 다양할 수 있는데, 배열 차원 크기에 따라 배열을 순회하기 위한 다양한 방법들이 있다.
1차원은 선형이므로 순회가 아주 쉽지만, 2차원부터는 여러 방법이 있다.
연습문제. 절대값의 합 구하기
순회와 탐색을 이용한 <연습문제. 절대값의="" 합="" 구하기="">를 풀어보자
- 5*5의 2차 배열에 무작위로 25개의 숫자로 초기화한 뒤 25개의 각 요소에 대해 그 요소와 이웃한 요소와의 차의 절대값을 구한 뒤 구한 모든 값의 총 합을 구한다.
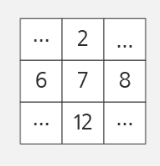
- 위 그림에서 7이 이웃한 네 개의 값과의 차의 절대값을 구해보면
|2–7|+|8–7|+|12–7|+|6–7| = 12가 된다. - 이 문제는 행 혹은 열 우선 순회를 돌면서 상하좌우에 있는 값과 비교하는 과정을 거치면 쉽게 해결 할 수 있다.
bool isWall(int x, int y) {
if (x < 0 || x >= 5) return true;
if (y < 0 || y >= 5) return true;
return false;
}
int calAbs(int a1, int a2) {
return(a1 - a2) > 0 ? (a1 - a2) : -(a1 - a2);
}
void main() {
int ary[][5] = {
{9,20,2,18,11},
{19,1,25,3,21},
{8,24,10,17,7},
{15,4,16,5,6},
{12,13,22,23,14} };
int dx[] = { 0,0,-1,1 };
int dy[] = {-1,1,0,0};
int newX,newY;
int sum =0;
for(int y=0; y < 5; y++){
for(int x=0; x < 5; x++){
for(int dir=0; dir < 4; dir++){
newX =x +dx[dir];
newY =y +dy[dir];
if(!isWall(newX,newY))
sum += calAbs(ary[y][x],ary[newY][newX]);
}
}
}
printf("sum = %d\n",sum);
}
isWall: outOfBound인지 검사calAbs: 절대값 계산- dx,dy로 상하좌우 인덱스를 이동시킬 수 있다. 좌표축에 따라 행 또는 열 우선 순회가 될 수 있다.
- 상하좌우 이동한 인덱스값을 구해 범위 내의 값인지 검사한 뒤 맞으면 절대값을 합해준다.
📑선택정렬
Selection Sort 선택 정렬이란 주어진 자료들 중 가장 작은 값의 원소부터 차례대로 선택해 위치를 교환하는 방법이다.
저장되어 있는 자료로부터 k번째로 큰 원소 혹은 작은 원소를 찾는 셀렉션 알고리즘 과정은
- 1번부터 k번째까지 작은 원소들을 찾아 배열을 앞쪽으로 이동, 배열의 k번째를 반환한다.
- k가 비교적 작을 때 유용하며 O(kn)의 수행시간을 필요로 한다.
정렬과정
- 주어진 리스트 중 최소값을 찾는다
- 그 값을 리스트 맨 앞에 위치한 값과 교환한다
- 맨 처음 위치를 제외한 나머지 리스트를 대상으로 위 과정을 반복한다
O(n^2)
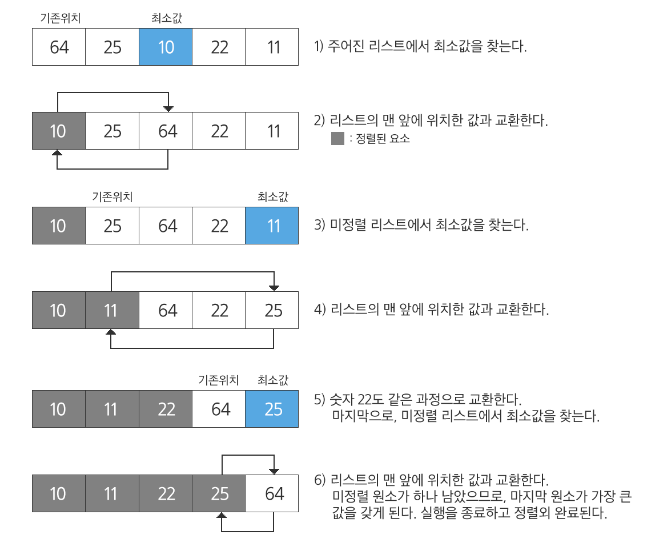
- 선택정렬은 버블이나 카운팅 정렬보다 교환의 회수가 작다.
⚙️대표문제 Ladder
사다리게임에서 꽝에 도착하게 되는 출발점을찾아라. 꽝은 2로 표시한다.
X=0 인 출발점에서 출발하는 사례에 대해서 화살표로 표시한 바와 같이, 아래 방향으로 진행하면서 좌우방향으로 이동가능한 통로가 나타나면 방향전환을 하게 된다.
방향 전환 이후엔 다시 아래 방향으로만 이동하게 되며, 바닥에 도착하면 멈추게 된다.문제의 X표시에 도착하려면 X=4 인 출발점에서 출발해야 하므로 답은 4가 된다.

입력
첫 번째 줄에 테스트 케이스 T(1<= T <= 100)가 주어진다. 각 테스트케이스 첫 줄에는 테스트 케이스 번호가 주어지고,
바로 다음 줄에는 테스트 케이스가 주어진다.
0으로 채워진 평면상에 사다리는 연속된 1로 표현된다. 도착지점은 2로 표현된다.
2
1
1001000000010000...
1001000000010000...
1001111111110000...
...
...
2
100100000100...
100111111100...
100100000100...
출력
X에 도착하게 되는 출발점의 X좌표를 출력한다.
67
3
해설
모든 출발점을 조사하는 대신, 목표지점에서부터 역추적하여 출발점으로 도착하는 방법을 채택하여 풀 것이다.
사다리 정보를 저장하기 위해서 2차원 배열을 사용하는데, 이 때 경계면에서 처리를 쉽게 하기 위해 여유 공간을 두어 배열을 생성한다.
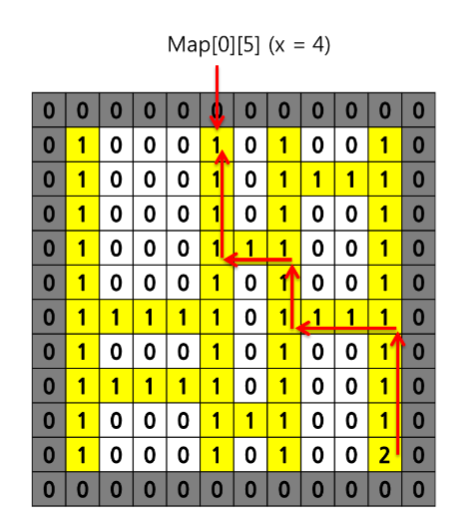
이런 여유를 두지 않으면 경계면을 넘는지 검사해야하는데,
메모리를 조금 아끼는 것보다 처리를 심플하게 하는 것이 더 중요하다
주어진 입력보다 조금 더 크게 배열을 잡는 경우가 미로찾기, 지뢰 찾기 등이 있다.
가장 먼저 도착점을 찾고 좌우를 살펴 길이 없으면 위로 올라간다. 좌우 길이 있으면 끝까지 이동하고 위로 올라가기를 반복한다.
Code
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define SIZE 102
void MapInit(int map[][SIZE]) {
int x, y;
int goal;
for (x = 0; x < SIZE; x++) {
for (y = 0; y < SIZE; y++) {
map[x][y] = 0;
}
for (x = 1; x < SIZE - 1; x++) {
for (y = 1; y < SIZE - 1; y++) {
int tmp; cin >> tmp;
map[x][y] = tmp;
}
}
}
}
int getGoal(int map[][SIZE]) {
int goal;
for (int y = 0; y < SIZE; y++) {
if (map[SIZE-2][y] == 2) {
goal = y;
break;
}
}
return goal;
}
int search(int map[][SIZE], int start) {
int x = SIZE - 2; int y = start;
while (x != 1) {
if (map[x][y - 1] == 1) {
while (map[x][y - 1] != 0) y--;
x--;
}
else if (map[x][y + 1] == 1) {
while (map[x][y + 1] != 0) y++;
x--;
}
else x--;
}
return y;
}
int main(void) {
int T; // testcase
cin >> T;
int Map[SIZE][SIZE]; // 경계면 여유 두기
int goal = 0;
for (int t = 0; t < T; t++) {
MapInit(Map); // 맵 초기화
goal = getGoal(Map); // 목표 지점이 되는 곳. 2 인 곳
}
cout << search(Map, goal) << endl; // 출발 지점 찾기
return 0;
}
- 헷갈리는 바람에 x와 y가 뒤바꼈다. 행이 y고 열이 x이어야 의미가 맞는데 위의 코드는 행이 x고 y가 열이 되었다.
- 코드는 간단하다. 먼저 경계면에 여유를 둔 맵 크기의 배열을 선언하고 맵을 초기화 해준다음, 2인 곳을 찾아주고 역으로 추적해주면 된다.
- 역으로 추적하는 코드는 왼쪽 오른쪽을 검사하고 1의 끝까지 이동한뒤 위로 한 칸 올라가주도록 작성했다.
1.5. 대표문제 평탄화
🔖대표문제 평탄화
한 쪽 벽면에 다음과 같이 노란색 상자들이 쌓여있었다.
높은 곳의 상자를 낮은 곳에 옮기는 방식으로 최고점과 최저점의 간격을 줄이는 작업을 평탄화라고 한다.
평탄화를 모두 수행하고 나면, 가장 높은 곳과 가장 낮은 곳의 차이가 최대 1이내가 된다.
평탄화 작업을 위해서 상자를 옮기는 작업 횟수에 제한이 걸려있을 때, 제한된 횟수만큼 옮기는 작업을 한 후, 최고점과 최저점의 차이를 리턴하는 함수를 구현하시오.
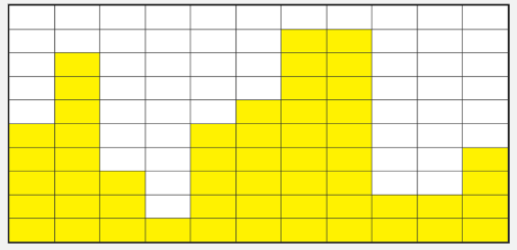
가장 높은 곳에 있는 상자를 가장 낮은 곳으로 옮기는 작업을 덤프라고 한다.
생각해봅시다
너무 어렵당…일단 차이를 줄이는 선택을 따라가야 할 것 같다.
각 열의 상자 개수들을 수집하여 가장 높은 상자를 가장 낮은 곳에 옮기는 과정을 제한된 횟수만큼 반복.
그 후 최고점과 최저점의 차이를 리턴한다.
이래서 덤프라는 정의를 문제에서 준 것 같다.
⚙️평탄화
입력
첫 번째 줄에는 덤프 횟수가 주어진다. 그리고 바로 다음 줄에 테스트 케이스가 주어진다.
총 10개의 테스트 케이스가 주어진다.
834
42 68 35 1 70 25 82 28 62 92 96 43 28 37 92 5 3 54 93 83 22 17 19 96...
617
16 40 59 5 31 2325 73 71 30 78 74 98 13 87 91 62 37 56 68 56 75 32 53...
출력
각 테스트케이스의 최고점과 최저점의 높이 차를 출력한다.
13
32
해설
- 상자 높이 중 최고 점을 찾는다
- 상자 높이 중 최하 점을 찾는다
- 찾아진 최고점에서 1 감소하고 찾아진 최하점에서 1 증가한다. 최고점과 최하점의 차이를 계산하여 반환한다.
Code
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define TESTCASE 1
#define COL 10
int getDiff(vector<int> v, int cnt) {
int max = v[0], min = v[0];
int maxIdx = 0, minIdx = 0;
while (cnt != 0) {
cnt--;
// 상자들 개수 중 최대 최소를 구한다
for (int i = 0; i < v.size(); i++) {
if (max < v[i]) {
max = v[i]; maxIdx = i;
}
if (min > v[i]) {
min = v[i]; minIdx = i;
}
}
// 개수를 --, ++ 해준다
v[maxIdx]--; v[minIdx]++;
if (v[maxIdx] - v[minIdx] <= 1) break;
}
max = v[0]; min = v[0];
for (int i = 0; i < v.size(); i++) {
if (max < v[i]) max = v[i];
if (min > v[i]) min = v[i];
}
return max - min;
}
int main(void) {
for (int t = 0; t < TESTCASE; t++) {
int dumpCount; cin >> dumpCount;
vector<int> boxes;
// 상자 채우기
for (int i = 0; i < COL; i++) {
int tmp; cin >> tmp;
boxes.push_back(tmp);
}
cout << getDiff(boxes, dumpCount) << endl;
}
return 0;
}