[LeetCode][C++] 437. Path Sum III

❓Question

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

✏️Example

• Example 1
  

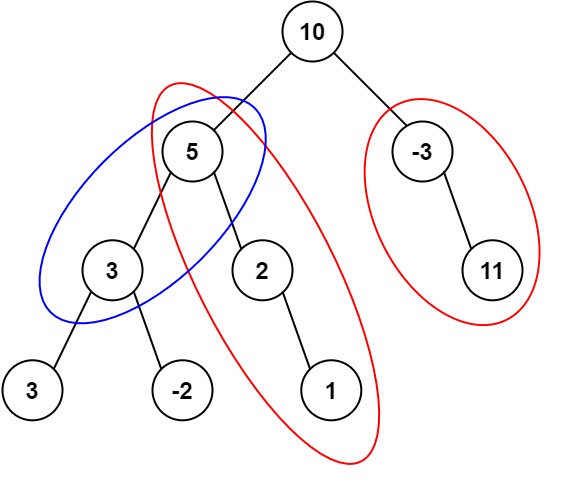
    Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
    Output: 3
    Explanation: The paths that sum to 8 are shown.
  

• Example 2

    Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
    Output: 3
  

---

• Constraints
  • The number of nodes in the tree is in the range [0, 1000].
  • -109 <= Node.val <= 109
  • -1000 <= targetSum <= 1000

---

👀Intuition

• First of all, we need to traverse all nodes of tree.
• And For each node, we need to get partial sums downwarding the children nodes including the relative root node.

👣Approach

1. We need to use dfs algorithm twice.
2. External DFS (pathSum): Traversing All Starting Nodes
   • The main dfs is to get count of Sum equals a given target traversing all the nodes of tree: pathSum
   • It calls the internal helper function (getSumCount) to count paths starting exactly at the current root.
   • It recursively calls itself (pathSum) on the left child (root->left) and right child (root->right). This ensures that the left and right children are also considered as new starting points for paths that don’t include the current root.
3. Internal DFS (getSumCount): Counting Paths Downwards
   • The Sub dfs is to get all the possible partial sum including for each node:getSumCount
   • It checks if the current node’s value equals the remaining target. If so, it counts the path.
   • It recursively calls itself on the left and right children, reducing the target by the current node’s val. This continues the path and tracks the remaining sum needed.

⏰Complexity

• Time complexity:

  The external dfs visits every node N times. For every node visited, the Internal dfs must explore every path starting from that node. Since N starting nodes explore up to N paths, the total time is O(N^2).

  However, for a balanced binary tree, the complexity is closer to O(NlogN).

• Space complexity:

  The space complexity is determined by the depth of the recursive call stack where H ist the height of the tree. O(H).

---

📚Solution

  /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
  class Solution {
  public:
      int pathSum(TreeNode* root, int targetSum) {
          if(!root) return 0;
          
          int count = getSumCount(root, (long long)targetSum);
          count += pathSum(root->left, targetSum);
          count += pathSum(root->right, targetSum);
          
          return count;
      }

      // including one node, get all possible sum through dfs 
      int getSumCount(TreeNode* root, long long target){
          if(!root) return 0;
          int count = 0;

          if(root->val == target) count=1;
          count += getSumCount(root->left, target - root->val);
          count += getSumCount(root->right, target - root->val);

          return count;
      }
      
  };